Dịch vụ SPSS tại Luận Văn Việt nổi bật với khả năng hỗ trợ đa dạng các nhu cầu phân tích số liệu, dữ liệu từ những nghiên cứu đơn giản đến các đề tài phức tạp, từ xử lý dữ liệu thô đến diễn giải kết quả chuyên sâu. Để hiểu rõ hơn về đội ngũ chuyên gia, giá cả, phạm vi, quy trình làm việc, cam kết chất lượng mà chúng tôi mang lại, hãy cùng Luận Văn Việt khám phá ngay trong bài viết https://luanvanviet.com/dich-vu-xu-ly-so-lieu-spss/
-
3 Posts
-
2 Photos
-
0 Videos
-
Lives in Hà Nội
-
From Vietnam
-
04/05/1966
-
Followed by 0 people
Recent Updates
-
Các Phương Pháp Thống Kê Mô Tả: Hướng Dẫn & Ứng Dụng Chi Tiết
Trong phân tích dữ liệu, việc nắm vững các phương pháp thống kê mô tả là vô cùng quan trọng. Bài viết này sẽ cung cấp cho bạn một hướng dẫn chi tiết về các phương pháp thống kê này, giúp bạn tóm tắt và mô tả dữ liệu một cách hiệu quả. Bạn đã bao giờ cảm thấy mình như lạc vào một mê cung dữ liệu, không biết bắt đầu từ đâu? Các phương pháp thống kê mô tả chính là chiếc la bàn giúp bạn định hướng, biến những con số khô khan thành những thông tin có ý nghĩa. Hãy cùng nhau khám phá nhé!
>> Đọc thêm: https://x.com/nghiavanspss
Thống Kê Mô Tả Là Gì?
Trước khi đi vào chi tiết về các phương pháp thống kê mô tả, chúng ta hãy cùng nhau nhắc lại một chút về khái niệm thống kê mô tả. Thống kê mô tả (descriptive statistics) là một nhánh của thống kê học, tập trung vào việc tóm tắt, mô tả và trình bày các đặc điểm chính của một tập dữ liệu. Mục tiêu chính của thống kê mô tả là giúp chúng ta hiểu rõ hơn về dữ liệu mà chúng ta đang có, thông qua việc sử dụng các số liệu thống kê, bảng biểu và đồ thị.
Khác với thống kê suy diễn (inferential statistics), vốn sử dụng dữ liệu mẫu để đưa ra kết luận về một tổng thể lớn hơn, thống kê mô tả chỉ tập trung vào việc mô tả các đặc trưng của chính dữ liệu đó. Nó không đưa ra bất kỳ suy luận hay dự đoán nào về một tổng thể.
Các bước cơ bản trong quá trình thống kê mô tả bao gồm:
Thu thập dữ liệu.
Xác định loại biến số (định tính, định lượng).
Tính toán các phép đo thống kê mô tả phù hợp.
Trình bày dữ liệu bằng bảng biểu và đồ thị.
Diễn giải ý nghĩa của kết quả.
Hiểu rõ về thống kê mô tả là nền tảng quan trọng để bạn có thể phân tích dữ liệu một cách hiệu quả.
>>> Xem tiếp: https://myspace.com/dichvuspss
Các Loại Biến Dữ Liệu Trong Thống Kê Mô Tả
Trước khi đi vào các kỹ thuật thống kê cụ thể, chúng ta cần hiểu rõ về các loại biến dữ liệu khác nhau. Việc xác định đúng loại biến sẽ giúp chúng ta chọn được các phương pháp phân tích phù hợp. Trong thống kê mô tả, chúng ta thường gặp hai loại biến dữ liệu chính:
Biến định tính (Qualitative Variables): Biến định tính mô tả các đặc điểm không phải là con số, mà là các thuộc tính, nhãn hiệu hoặc danh mục. Các biến này có thể chia thành:
Biến định danh (Nominal Variables): Biến định danh chỉ phân loại đối tượng vào các nhóm khác nhau mà không có thứ tự nào cả. Ví dụ: giới tính (nam, nữ), màu sắc (đỏ, xanh, vàng), loại phương tiện (ô tô, xe máy, xe đạp).
Biến thứ bậc (Ordinal Variables): Biến thứ bậc cũng phân loại đối tượng vào các nhóm, nhưng các nhóm này có thứ tự. Ví dụ: mức độ hài lòng (rất hài lòng, hài lòng, bình thường, không hài lòng), trình độ học vấn (tiểu học, trung học, đại học).
Biến định lượng (Quantitative Variables): Biến định lượng mô tả các đặc điểm bằng con số. Các biến này có thể chia thành:
Biến khoảng (Interval Variables): Biến khoảng đo lường bằng con số, có khoảng cách bằng nhau giữa các giá trị, nhưng không có điểm 0 tuyệt đối. Ví dụ: nhiệt độ đo bằng độ C, năm sinh.
Biến tỷ lệ (Ratio Variables): Biến tỷ lệ có tất cả các đặc điểm của biến khoảng, nhưng có thêm điểm 0 tuyệt đối. Ví dụ: chiều cao, cân nặng, thu nhập, số lượng sản phẩm.
Việc nắm vững các loại biến dữ liệu này giúp chúng ta chọn đúng các phương pháp thống kê phù hợp và diễn giải kết quả một cách chính xác.
Tìm hiểu thêm tại: https://padlet.com/dichvuspss
#dichvuspss #diachitimdichvuspss #websitedichvuspss #uytin #lvv #phuongphapthongkemotaCác Phương Pháp Thống Kê Mô Tả: Hướng Dẫn & Ứng Dụng Chi Tiết Trong phân tích dữ liệu, việc nắm vững các phương pháp thống kê mô tả là vô cùng quan trọng. Bài viết này sẽ cung cấp cho bạn một hướng dẫn chi tiết về các phương pháp thống kê này, giúp bạn tóm tắt và mô tả dữ liệu một cách hiệu quả. Bạn đã bao giờ cảm thấy mình như lạc vào một mê cung dữ liệu, không biết bắt đầu từ đâu? Các phương pháp thống kê mô tả chính là chiếc la bàn giúp bạn định hướng, biến những con số khô khan thành những thông tin có ý nghĩa. Hãy cùng nhau khám phá nhé! >> Đọc thêm: https://x.com/nghiavanspss Thống Kê Mô Tả Là Gì? Trước khi đi vào chi tiết về các phương pháp thống kê mô tả, chúng ta hãy cùng nhau nhắc lại một chút về khái niệm thống kê mô tả. Thống kê mô tả (descriptive statistics) là một nhánh của thống kê học, tập trung vào việc tóm tắt, mô tả và trình bày các đặc điểm chính của một tập dữ liệu. Mục tiêu chính của thống kê mô tả là giúp chúng ta hiểu rõ hơn về dữ liệu mà chúng ta đang có, thông qua việc sử dụng các số liệu thống kê, bảng biểu và đồ thị. Khác với thống kê suy diễn (inferential statistics), vốn sử dụng dữ liệu mẫu để đưa ra kết luận về một tổng thể lớn hơn, thống kê mô tả chỉ tập trung vào việc mô tả các đặc trưng của chính dữ liệu đó. Nó không đưa ra bất kỳ suy luận hay dự đoán nào về một tổng thể. Các bước cơ bản trong quá trình thống kê mô tả bao gồm: Thu thập dữ liệu. Xác định loại biến số (định tính, định lượng). Tính toán các phép đo thống kê mô tả phù hợp. Trình bày dữ liệu bằng bảng biểu và đồ thị. Diễn giải ý nghĩa của kết quả. Hiểu rõ về thống kê mô tả là nền tảng quan trọng để bạn có thể phân tích dữ liệu một cách hiệu quả. >>> Xem tiếp: https://myspace.com/dichvuspss Các Loại Biến Dữ Liệu Trong Thống Kê Mô Tả Trước khi đi vào các kỹ thuật thống kê cụ thể, chúng ta cần hiểu rõ về các loại biến dữ liệu khác nhau. Việc xác định đúng loại biến sẽ giúp chúng ta chọn được các phương pháp phân tích phù hợp. Trong thống kê mô tả, chúng ta thường gặp hai loại biến dữ liệu chính: Biến định tính (Qualitative Variables): Biến định tính mô tả các đặc điểm không phải là con số, mà là các thuộc tính, nhãn hiệu hoặc danh mục. Các biến này có thể chia thành: Biến định danh (Nominal Variables): Biến định danh chỉ phân loại đối tượng vào các nhóm khác nhau mà không có thứ tự nào cả. Ví dụ: giới tính (nam, nữ), màu sắc (đỏ, xanh, vàng), loại phương tiện (ô tô, xe máy, xe đạp). Biến thứ bậc (Ordinal Variables): Biến thứ bậc cũng phân loại đối tượng vào các nhóm, nhưng các nhóm này có thứ tự. Ví dụ: mức độ hài lòng (rất hài lòng, hài lòng, bình thường, không hài lòng), trình độ học vấn (tiểu học, trung học, đại học). Biến định lượng (Quantitative Variables): Biến định lượng mô tả các đặc điểm bằng con số. Các biến này có thể chia thành: Biến khoảng (Interval Variables): Biến khoảng đo lường bằng con số, có khoảng cách bằng nhau giữa các giá trị, nhưng không có điểm 0 tuyệt đối. Ví dụ: nhiệt độ đo bằng độ C, năm sinh. Biến tỷ lệ (Ratio Variables): Biến tỷ lệ có tất cả các đặc điểm của biến khoảng, nhưng có thêm điểm 0 tuyệt đối. Ví dụ: chiều cao, cân nặng, thu nhập, số lượng sản phẩm. Việc nắm vững các loại biến dữ liệu này giúp chúng ta chọn đúng các phương pháp thống kê phù hợp và diễn giải kết quả một cách chính xác. Tìm hiểu thêm tại: https://padlet.com/dichvuspss #dichvuspss #diachitimdichvuspss #websitedichvuspss #uytin #lvv #phuongphapthongkemota0 Comments 0 Shares 147 Views 0 ReviewsPlease log in to like, share and comment! -
Đo Lường Trung Tâm trong thống kê mô tả
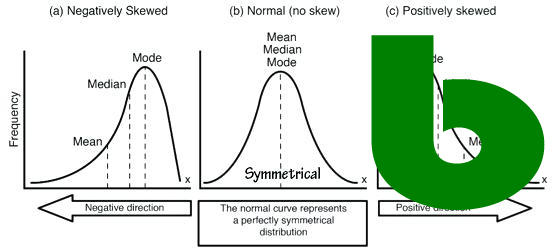
Trong thống kê mô tả, đo lường trung tâm giúp chúng ta xác định vị trí trung tâm của dữ liệu. Chúng ta sẽ cùng nhau tìm hiểu chi tiết hơn về mean, median và mode.
Mean (Trung bình):
Cách tính: Cộng tất cả các giá trị trong tập dữ liệu rồi chia cho số lượng giá trị.
Ưu điểm: Dễ tính toán và dễ hiểu.
Nhược điểm: Bị ảnh hưởng bởi các giá trị ngoại lai (outliers). Ví dụ, nếu có một vài giá trị quá lớn hoặc quá nhỏ, trung bình sẽ bị kéo lệch về phía đó.
Sử dụng khi: Dữ liệu có phân phối đối xứng và không có giá trị ngoại lai.
Median (Trung vị):
Cách tính: Sắp xếp dữ liệu theo thứ tự từ nhỏ đến lớn. Giá trị ở giữa là trung vị. Nếu số lượng giá trị là số chẵn, trung vị là trung bình cộng của hai giá trị ở giữa.
Ưu điểm: Không bị ảnh hưởng bởi các giá trị ngoại lai, thích hợp cho dữ liệu có phân phối lệch.
Nhược điểm: Khó tính toán hơn mean.
Sử dụng khi: Dữ liệu có phân phối lệch hoặc có giá trị ngoại lai.
Mode (Mốt):
Cách tính: Giá trị xuất hiện nhiều lần nhất trong tập dữ liệu.
Ưu điểm: Dễ xác định, đặc biệt hữu ích cho biến định tính.
Nhược điểm: Có thể có nhiều mốt hoặc không có mốt.
Sử dụng khi: Quan tâm đến giá trị phổ biến nhất trong dữ liệu
Tìm hiểu thêm tại: https://www.pinterest.com/dichvuchayspss/
Ví dụ: Giả sử chúng ta có dữ liệu về số giờ làm việc một tuần của 5 người: 30, 40, 40, 45, 60.
Mean = (30 + 40 + 40 + 45 + 60) / 5 = 43
Median = 40
Mode = 40
Trong trường hợp này, trung bình bị ảnh hưởng bởi giá trị 60, trong khi trung vị và mốt vẫn cho thấy phần lớn mọi người làm việc quanh 40 giờ/tuần.
Hiểu rõ sự khác biệt giữa mean, median và mode giúp bạn lựa chọn được đo lường trung tâm phù hợp với dữ liệu của mình.
>>> Xem tiếp: https://myspace.com/dichvuspss
Để tiếp tục tìm hiểu về Đo Lường Trung Tâm và ứng dụng của chúng, hãy cùng đón đọc phần tiếp theo của bài viết. Bạn cũng có thể xem thêm các kiến thức về thống kê trên Luận Văn Việt về Thống Kê để hiểu sâu hơn.
Đọc thêm: https://x.com/nghiavanspssĐo Lường Trung Tâm trong thống kê mô tả Trong thống kê mô tả, đo lường trung tâm giúp chúng ta xác định vị trí trung tâm của dữ liệu. Chúng ta sẽ cùng nhau tìm hiểu chi tiết hơn về mean, median và mode. Mean (Trung bình): Cách tính: Cộng tất cả các giá trị trong tập dữ liệu rồi chia cho số lượng giá trị. Ưu điểm: Dễ tính toán và dễ hiểu. Nhược điểm: Bị ảnh hưởng bởi các giá trị ngoại lai (outliers). Ví dụ, nếu có một vài giá trị quá lớn hoặc quá nhỏ, trung bình sẽ bị kéo lệch về phía đó. Sử dụng khi: Dữ liệu có phân phối đối xứng và không có giá trị ngoại lai. Median (Trung vị): Cách tính: Sắp xếp dữ liệu theo thứ tự từ nhỏ đến lớn. Giá trị ở giữa là trung vị. Nếu số lượng giá trị là số chẵn, trung vị là trung bình cộng của hai giá trị ở giữa. Ưu điểm: Không bị ảnh hưởng bởi các giá trị ngoại lai, thích hợp cho dữ liệu có phân phối lệch. Nhược điểm: Khó tính toán hơn mean. Sử dụng khi: Dữ liệu có phân phối lệch hoặc có giá trị ngoại lai. Mode (Mốt): Cách tính: Giá trị xuất hiện nhiều lần nhất trong tập dữ liệu. Ưu điểm: Dễ xác định, đặc biệt hữu ích cho biến định tính. Nhược điểm: Có thể có nhiều mốt hoặc không có mốt. Sử dụng khi: Quan tâm đến giá trị phổ biến nhất trong dữ liệu Tìm hiểu thêm tại: https://www.pinterest.com/dichvuchayspss/ Ví dụ: Giả sử chúng ta có dữ liệu về số giờ làm việc một tuần của 5 người: 30, 40, 40, 45, 60. Mean = (30 + 40 + 40 + 45 + 60) / 5 = 43 Median = 40 Mode = 40 Trong trường hợp này, trung bình bị ảnh hưởng bởi giá trị 60, trong khi trung vị và mốt vẫn cho thấy phần lớn mọi người làm việc quanh 40 giờ/tuần. Hiểu rõ sự khác biệt giữa mean, median và mode giúp bạn lựa chọn được đo lường trung tâm phù hợp với dữ liệu của mình. >>> Xem tiếp: https://myspace.com/dichvuspss Để tiếp tục tìm hiểu về Đo Lường Trung Tâm và ứng dụng của chúng, hãy cùng đón đọc phần tiếp theo của bài viết. Bạn cũng có thể xem thêm các kiến thức về thống kê trên Luận Văn Việt về Thống Kê để hiểu sâu hơn. Đọc thêm: https://x.com/nghiavanspss0 Comments 0 Shares 56 Views 0 Reviews -
0 Comments 0 Shares 21 Views 0 Reviews
More Stories